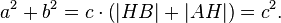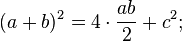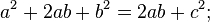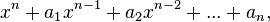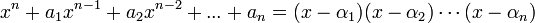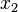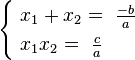| Статистика |
Полная статистика
Онлайн всего: 1 Гостей: 1 Пользователей: 0
Онлайн всего: 1 Гостей: 1 Пользователей: 0
|
|
Каталог интересных статей
Основная теоремы, история, доказательства, применения
- Теорема Ролля
- Теорема Пифагора
- Формулы Виета
Теоре́ма (др.-греч. θεώρημα — «зрелище, вид; взгляд; представление, положение») — утверждение, для которого в рассматриваемой теории существует доказательство (иначе говоря, вывод). В отличие от теорем, аксиомами называются утверждения, которые, в рамках конкретной теории, принимаются истинными без всяких доказательств или обоснований.
В математических текстах теоремами обычно называют только достаточно важные утверждения. При этом требуемые доказательства обычно кем-либо найдены (исключение составляют в основном работы по логике, в которых изучается само понятие доказательства, а потому в некоторых случаях теоремами называют даже неопределённые утверждения). Менее важные утверждения-теоремы обычно называют леммами, предложениями, следствиями, условиями и прочими подобными терминами. Утверждения, о которых неизвестно, являются ли они теоремами, обычно называют гипотезами.
Теорема Ролля
Теорема Ро́лля (теорема о нуле производной) утверждает, что
Если вещественная функция непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b), принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю.  Геометрический смысл Геометрический смысл Теорема утверждает, что если ординаты обоих концов гладкой кривой равны, то на кривой найдется точка, в которой касательная к кривой параллельна оси абсцисс. Следствие Если непрерывная функция обращается в ноль в n различных точках, то ее производная обращается в ноль по крайней мере в n − 1 различных точках[1], причем эти нули производной лежат в выпуклой оболочке нулей исходной функции. Это следствие легко проверяется для случая действительных корней, однако имеет место и в комплексном случае.
Теорема Пифагора-история, доказательства, применения
Формулировки
Геометрическая формулировка: Изначально теорема была сформулирована следующим образом: В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.
Алгебраическая формулировка: В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
То есть, обозначив длину гипотенузы треугольника через c, а длины катетов через a и b: a2 + b2 = c2 Обе формулировки теоремы эквивалентны, но вторая формулировка более элементарна, она не требует понятия площади. То есть второе утверждение можно проверить, ничего не зная о площади и измерив только длины сторон прямоугольного треугольника.
Обратная теорема Пифагора: Для всякой тройки положительных чисел a, b и c, такой, что a2 + b2 = c2, существует прямоугольный треугольник с катетами a и b и гипотенузой c.
ДоказательстваНа данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии. Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них: доказательства методом площадей, аксиоматические и экзотические доказательства (например, с помощью дифференциальных уравнений). Через подобные треугольникиСледующее доказательство алгебраической формулировки — наиболее простое из доказательств, строящихся напрямую из аксиом. В частности, оно не использует понятие площади фигуры.
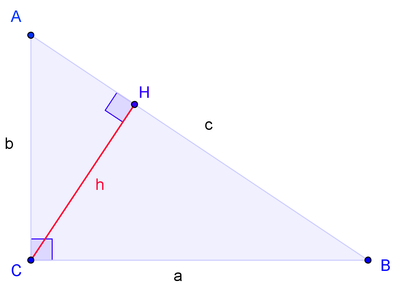
Пусть ABC есть прямоугольный треугольник с прямым углом C. Проведём высоту из C и обозначим её основание через H. Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC. Введя обозначения | BC | = a, | AC | = b, | AB | = c получаем 
Что эквивалентно 
Сложив, получаем 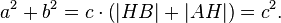
или a2 + b2 = c2, что и требовалось доказать
Доказательства методом площадей Ниже приведённые доказательства, несмотря на их кажущуюся простоту, вовсе не такие простые. Все они используют свойства площади, доказательства которых сложнее доказательства самой теоремы Пифагора.
Доказательство через равнодополняемость
- Расположим четыре равных прямоугольных треугольника так, как показано на рисунке 1.
- Четырёхугольник со сторонами c является квадратом, так как сумма двух острых углов 90°, а развёрнутый угол — 180°.
- Площадь всей фигуры равна, с одной стороны, площади квадрата со стороной (a+b), а с другой стороны, сумме площадей четырёх треугольников и площади внутреннего квадрата.
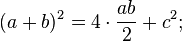 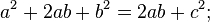 
Что и требовалось доказать. История
В древнекитайской книге Чу-пей (англ.) (кит. 周髀算經) говорится о пифагоровом треугольнике со сторонами 3, 4 и 5. В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары. Мориц Кантор (крупнейший немецкий историк математики) считает, что равенство 3 ² + 4 ² = 5² было известно уже египтянам ещё около 2300 г. до н. э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея). По мнению Кантора, гарпедонапты, или «натягиватели верёвок», строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5. Очень легко можно воспроизвести их способ построения. Возьмём верёвку длиною в 12 м и привяжем к ней по цветной полоске на расстоянии 3 м от одного конца и 4 метра от другого. Прямой угол окажется заключённым между сторонами длиной в 3 и 4 метра. Гарпедонаптам можно было бы возразить, что их способ построения становится излишним, если воспользоваться, например, деревянным угольником, применяемым всеми плотниками. И действительно, известны египетские рисунки, на которых встречается такой инструмент, — например, рисунки, изображающие столярную мастерскую. Несколько больше известно о теореме Пифагора у вавилонян. В одном тексте, относимом ко времени Хаммурапи, то есть к 2000 году до н. э., приводится приближённое вычисление гипотенузы прямоугольного треугольника. Отсюда можно сделать вывод, что в Двуречье умели производить вычисления с прямоугольными треугольниками, по крайней мере в некоторых случаях. Основываясь, с одной стороны, на сегодняшнем уровне знаний о египетской и вавилонской математике, а с другой — на критическом изучении греческих источников, Ван-дер-Варден (голландский математик) сделал вывод о большой вероятности того, что теорема о квадрате гипотенузы была известна в Индии уже около XVIII века до н. э. Согласно комментарию Прокла к Евклиду, Пифагор (годами жизни которого принято считать 570—490 гг. до н. э.) использовал алгебраические методы, чтобы находить пифагоровы тройки. Однако Прокл писал между 410 и 485 гг. н. э. Томас Литтл Хит (en:Thomas Little Heath) считал, что не существует явного упоминания, относящегося к периоду продолжительностью 5 веков после смерти Пифагора, что Пифагор был автором теоремы.Однако, когда авторы, такие как Плутарх и Цицерон, пишут о теореме Пифагора, они пишут так, как будто авторство Пифагора было широко известным и несомненным.«Принадлежит ли эта формула лично перу Пифагора…, но мы можем уверенно считать, что она принадлежит древнейшему периоду пифагорейской математики». По преданию, Пифагор отпраздновал открытие своей теоремы гигантским пиром, заклав на радостях сотню быков. Приблизительно в 400 г. до н. э., согласно Проклу, Платон дал метод нахождения пифагоровых троек, сочетающий алгебру и геометрию. Приблизительно в 300 г. до н. э. в «Началах» Евклида появилось старейшее аксиоматическое доказательство теоремы Пифагора.
Формулы Виета
Формулы Виета — формулы, выражающие коэффициенты многочлена через его корни. Этими формулами удобно пользоваться для проверки правильности нахождения корней многочлена, а также для составления многочлена по заданным его корням.
ФормулировкаЕсли  — корни многочлена — корни многочлена 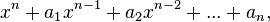
(каждый корень взят соответствующее его кратности число раз), то коэффициенты  выражаются в виде симметрических многочленов от корней, а именно:

Иначе говоря ( − 1)kak равно сумме всех возможных произведений из k корней. Если старший коэффициент многочлена  , то для применения формулы Виета необходимо предварительно разделить все коэффициенты на a0 (это не влияет на значение корней многочлена). В этом случае формулы Виета дают выражение для отношений всех коэффициентов к старшему. Из последней формулы Виета следует, что если корни многочлена целочисленные, то они являются делителями его свободного члена, который также целочисленный. , то для применения формулы Виета необходимо предварительно разделить все коэффициенты на a0 (это не влияет на значение корней многочлена). В этом случае формулы Виета дают выражение для отношений всех коэффициентов к старшему. Из последней формулы Виета следует, что если корни многочлена целочисленные, то они являются делителями его свободного члена, который также целочисленный.
ДоказательствоДоказательство осуществляется рассмотрением равенства, полученного разложением многочлена по корням, учитывая, что a0 = 1 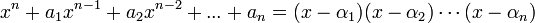
Приравнивая коэффициенты при одинаковых степенях x (теорема единственности), получаем формулы Виета.
ПримерыКвадратное уравнениеСумма корней приведенного квадратного уравнения равна второму коэффициенту с обратным знаком, а произведение корней равно свободному члену. Иными словами, если  и и 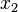 — корни квадратного уравнения — корни квадратного уравнения  ,то ,то 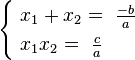
В частном случае, если a = 1 (приведенная форма x2 + px + q = 0), то  . .
Кубическое уравнение
Если x1,x2,x3 — корни кубического уравнения p(x) = ax3 + bx2 + cx + d = 0, то 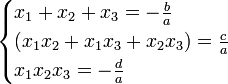
|
| Категория: Общее | Добавил: Админ)) (08.02.2012)
|
| Просмотров: 2076
| Рейтинг: 0.0/0 |
Добавлять комментарии могут только зарегистрированные пользователи. [ Регистрация | Вход ] |
|
 СЧАСТЛИВЫ ВМЕСТЕ
СЧАСТЛИВЫ ВМЕСТЕ АЙКАРЛИ
АЙКАРЛИ Наруто
Наруто ФУТУРАМА
ФУТУРАМА Интерны
Интерны ДАЕШЬ МОЛОДЕЖЬ!
ДАЕШЬ МОЛОДЕЖЬ! Тетрадь смерти
Тетрадь смерти Пороблено в Україні
Пороблено в Україні Симпсоны
Симпсоны ЮЖНЫЙ ПАРК
ЮЖНЫЙ ПАРК Эльфийская песнь
Эльфийская песнь Пингвины из Мадагаскара
Пингвины из Мадагаскара Друзья
Друзья Блич
Блич  Южное Бутово
Южное Бутово 
 М/С Звездные войны/Star wars
М/С Звездные войны/Star wars  Солдаты
Солдаты Кремлевские курсанты
Кремлевские курсанты